Exercices d'algorithmiques.

Écris une fonction occurrences(caractere, chaine) qui prend en paramètres :

• caractere : une chaîne de longueur 1,
• chaine : une chaîne de caractères,

et retourne le nombre de fois où caractere apparaît dans chaine.

⭐ Exemples :

>>> occurrences('e', "sciences")
2
>>> occurrences('i', "mississippi")
4
>>> occurrences('a', "mississippi")
0

Écris une fonction compte_occurrences(x, tab) qui prend en paramètres :

• x : une valeur,
• tab : une liste,

et retourne le nombre d’occurrences de x dans tab.

⚠️ Il est interdit d’utiliser la méthode count des listes Python.

⭐ Exemples :

>>> compte_occurrences(5, [])
0
>>> compte_occurrences(5, [-2, 3, 1, 5, 3, 7, 4])
1
>>> compte_occurrences('a', ['a','b','c','a','d','e','a'])
3

Écris une fonction maximum_tableau(tab) qui prend en paramètre une liste non vide de nombres tab et retourne le plus grand élément de cette liste.

⭐ Exemple :

>>> maximum_tableau([98, 12, 104, 23, 131, 9])
131
>>> maximum_tableau([-27, 24, -3, 15])
24

Écris une fonction nb_repetitions(elt, tab) qui prend en paramètres :

• elt : un élément,
• tab : une liste d’éléments du même type,

et retourne le nombre de fois où elt apparaît dans tab.

⭐ Exemples :

>>> nb_repetitions(5, [2, 5, 3, 5, 6, 9, 5])
3
>>> nb_repetitions('A', ['B', 'A', 'B', 'A', 'R'])
2
>>> nb_repetitions(12, [1, '!', 7, 21, 36, 44])
0

Écris une fonction verifie(tab) qui prend en paramètre une liste de valeurs numériques et retourne True si la liste est triée dans l’ordre croissant, False sinon.

Un tableau vide est considéré comme trié.

⭐ Exemples :

>>> verifie([0, 5, 8, 9])
True
>>> verifie([8, 12, 4])
False
>>> verifie([-1, 4])
True
>>> verifie([])
True
>>> verifie([5])
True

On considère des tables (des listes de dictionnaires) qui contiennent des enregistrements relatifs à des animaux hébergés dans un refuge. Les attributs de chaque enregistrement sont 'nom', 'espece', 'age', 'enclos'.

Exemple :

animaux = [
    {'nom':'Medor', 'espece':'chien', 'age':5, 'enclos':2},
    {'nom':'Titine', 'espece':'chat', 'age':2, 'enclos':5},
    {'nom':'Tom', 'espece':'chat', 'age':7, 'enclos':4},
    {'nom':'Belle', 'espece':'chien', 'age':6, 'enclos':3},
    {'nom':'Mirza', 'espece':'chat', 'age':6, 'enclos':5}
]

Programme une fonction selection_enclos(table_animaux, num_enclos) qui :

• prend en paramètres une table table_animaux (liste de dictionnaires) et un numéro d’enclos num_enclos,
• renvoie une nouvelle table contenant uniquement les enregistrements dont l’attribut 'enclos' est égal à num_enclos.

⭐ Exemples :

>>> selection_enclos(animaux, 5)
[{'nom':'Titine', 'espece':'chat', 'age':2, 'enclos':5},
 {'nom':'Mirza', 'espece':'chat', 'age':6, 'enclos':5}]

>>> selection_enclos(animaux, 2)
[{'nom':'Medor', 'espece':'chien', 'age':5, 'enclos':2}]

>>> selection_enclos(animaux, 7)
[]

Programme une fonction renverse(mot) qui prend en paramètre une chaîne de caractères mot et retourne cette chaîne en ordre inverse.

⭐ Exemples :

>>> renverse("")
""
>>> renverse("abc")
"cba"
>>> renverse("informatique")
"euqitamrofni"

Un palindrome se lit de la même façon de gauche à droite ou de droite à gauche.

Exemples de mots palindromes : bob, radar, non.

Exemples de nombres palindromes : 33, 121, 345543.

Complète les trois fonctions ci-dessous :

• inverse_chaine : inverse une chaîne de caractères et renvoie la chaîne inversée ;
• est_palindrome : renvoie True si la chaîne est un palindrome, False sinon ;
• est_nbre_palindrome : renvoie True si un nombre est palindrome, False sinon.

⭐ Exemples :

>>> inverse_chaine('bac')
'cab'
>>> est_palindrome('NSI')
False
>>> est_palindrome('ISN-NSI')
True
>>> est_nbre_palindrome(214312)
False
>>> est_nbre_palindrome(213312)
True

Écris une fonction recherche(elt, tab) qui prend en paramètres :

• elt : un nombre entier
• tab : une liste d’entiers

La fonction doit retourner l’indice de la première occurrence de elt dans tab si elt est présent, et None sinon.

⚠️ Il est interdit d’utiliser la méthode index() de Python : la solution doit parcourir la liste avec une boucle.

⭐ Exemples :

>>> recherche(1, [2, 3, 4])
None
>>> recherche(1, [10, 12, 1, 56])
2
>>> recherche(50, [1, 50, 1])
1
>>> recherche(15, [8, 9, 10, 15])
3

Écris une fonction recherche(elt, tab) qui prend en paramètres :

• elt : un entier,
• tab : une liste d’entiers,

et retourne l’indice de la dernière occurrence de elt dans tab si elt est présent, ou None sinon.

⭐ Exemples :

>>> recherche(1, [2, 3, 4])
None
>>> recherche(1, [10, 12, 1, 56])
2
>>> recherche(1, [1, 0, 42, 7])
0
>>> recherche(1, [1, 50, 1])
2
>>> recherche(1, [8, 1, 10, 1, 7, 1, 8])
5

On considère des mots à trous : ce sont des chaînes de caractères contenant uniquement des majuscules et des caractères '*'. Par exemple 'INFO*MA*IQUE', '***I***E**' et '*S*' sont des mots à trous.

Programme une fonction correspond(mot, mot_a_trous) qui :

• prend en paramètres deux chaînes de caractères mot et mot_a_trous,
• renvoie True si on peut obtenir mot en remplaçant convenablement les caractères '*' de mot_a_trous,
• renvoie False sinon.

⭐ Exemples :

>>> correspond("INFORMATIQUE", "INFO*MA*IQUE")
True
>>> correspond("AUTOMATIQUE", "INFO*MA*IQUE")
False
>>> correspond("STOP", "S*")
False
>>> correspond("AUTO", "*UT*")
True

Écris une fonction enumere(tab) qui prend en paramètre une liste tab et renvoie un dictionnaire dont :

• les clés sont les éléments de tab,
• les valeurs sont les listes des indices où apparaissent ces éléments dans tab.

⭐ Exemples :

>>> enumere([])
{}
>>> enumere([1, 2, 3])
{1: [0], 2: [1], 3: [2]}
>>> enumere([1, 1, 2, 3, 2, 1])
{1: [0, 1, 5], 2: [2, 4], 3: [3]}   

Le nombre d’occurrences d’un caractère dans une chaîne de caractères est le nombre d’apparitions de ce caractère dans la chaîne.

Exemples :

• le nombre d’occurrences du caractère 'o' dans 'bonjour' est 2 ;
• le nombre d’occurrences du caractère 'b' dans 'Bébé' est 1 ;
• le nombre d’occurrences du caractère 'B' dans 'Bébé' est 1 ;
• le nombre d’occurrences du caractère ' ' dans 'Hello world !' est 2.

On souhaite écrire une fonction nbr_occurrences(chaine) qui construit un dictionnaire dont :

• les clés sont les caractères de chaine,
• les valeurs sont le nombre d’occurrences de chaque caractère.

⭐ Exemple :

>>> nbr_occurrences("Hello world !")
{'H': 1, 'e': 1, 'l': 3, 'o': 2, ' ': 2, 'w': 1, 'r': 1, 'd': 1, '!': 1}

L’ordre des clés dans le dictionnaire n’a pas d’importance.

L'opérateur « ou exclusif » entre deux bits renvoie 0 si les deux bits sont égaux et 1 s'ils sont différents. Il est symbolisé par le caractère \( \oplus \).

Ainsi :

• \( 0 \oplus 0 = 0 \)
• \( 0 \oplus 1 = 1 \)
• \( 1 \oplus 0 = 1 \)
• \( 1 \oplus 1 = 0 \)

On représente ici une suite de bits par un tableau contenant des 0 et des 1.

Exemples :

a = [1, 0, 1, 0, 1, 1, 0, 1]
b = [0, 1, 1, 1, 0, 1, 0, 0]
c = [1, 1, 0, 1]
d = [0, 0, 1, 1]

Écris la fonction ou_exclusif qui prend en paramètres deux tableaux de même longueur et qui renvoie un tableau où l’élément situé à la position i est le résultat de \( tab1[i] \oplus tab2[i] \).

Avec les exemples ci-dessus, cette fonction doit donner :

>>> ou_exclusif(a, b)
[1, 1, 0, 1, 1, 0, 0, 1]
>>> ou_exclusif(c, d)
[1, 1, 1, 0]

Le codage par différence (delta encoding en anglais) permet de compresser un tableau de données en indiquant pour chaque valeur sa différence avec la précédente (plutôt que la valeur elle-même). Cette méthode est efficace lorsque les valeurs consécutives sont proches.

Écris la fonction delta(liste) qui prend en paramètre une liste non vide d’entiers et renvoie la liste compressée avec cette technique.

⭐ Exemples :

>>> delta([1000, 800, 802, 1000, 1003])
[1000, -200, 2, 198, 3]
>>> delta([42])
[42]

On a relevé les valeurs moyennes annuelles des températures à Paris pour la période 2013–2019. Les résultats sont stockés dans deux listes : l’une pour les températures, l’autre pour les années.

t_moy = [14.9, 13.3, 13.1, 12.5, 13.0, 13.6, 13.7]
annees = [2013, 2014, 2015, 2016, 2017, 2018, 2019]

Écris la fonction annee_temperature_minimale qui prend en paramètres ces deux listes et qui renvoie la plus petite température relevée au cours de la période et l’année correspondante.

On suppose que la température minimale est atteinte une seule fois.

⭐ Exemple :

>>> annee_temperature_minimale(t_moy, annees)
(12.5, 2016)

On appelle « mot » une chaîne composée uniquement de lettres (minuscules ou majuscules).

On appelle « phrase » une chaîne qui :

• est composée d’un ou plusieurs mots séparés par un espace ' ',
• se termine :
  • soit par un point '.' collé au dernier mot,
  • soit par un point d’exclamation '!' ou d’interrogation '?' séparé du dernier mot par un espace.

Exemples de phrases :

• 'Cet exercice est simple.'
• 'Le point d exclamation est separe !'

Programme la fonction nombre_de_mots qui prend en paramètre une phrase et renvoie le nombre de mots qu’elle contient.

⭐ Exemples :

>>> nombre_de_mots('Cet exercice est simple.')
4
>>> nombre_de_mots('Le point d exclamation est separe !')
6
>>> nombre_de_mots('Combien de mots y a t il dans cette phrase ?')
10
>>> nombre_de_mots('Fin.')
1

Écris une fonction recherche_min qui prend en paramètre une liste tab non vide de nombres (non triés) et qui renvoie l’indice de la première occurrence du minimum de la liste.

⭐ Exemples :

>>> recherche_min([5])
0
>>> recherche_min([2, 4, 1])
2
>>> recherche_min([5, 3, 2, 2, 4])
2
>>> recherche_min([-1, -2, -3, -3])
2

Écris une fonction indices_maxi qui prend en paramètre une liste tab non vide de nombres entiers et qui renvoie un couple :

• le plus grand élément de la liste,
• la liste des indices où ce maximum apparaît dans tab.

⭐ Exemples :

>>> indices_maxi([1, 5, 6, 9, 1, 2, 3, 7, 9, 8])
(9, [3, 8])
>>> indices_maxi([7])
(7, [0])

Écris une fonction a_doublon qui prend en paramètre une liste triée de nombres et renvoie True si la liste contient au moins deux nombres identiques, False sinon.

⭐ Exemples :

>>> a_doublon([])
False
>>> a_doublon([1])
False
>>> a_doublon([1, 2, 4, 6, 6])
True
>>> a_doublon([2, 5, 7, 7, 7, 9])
True
>>> a_doublon([0, 2, 3])
False

Écris une fonction ajoute_dictionnaires qui prend en paramètres deux dictionnaires d1 et d2 dont les clés sont des nombres, et qui renvoie un dictionnaire d défini ainsi :

• Les clés de d sont celles de d1 et d2 réunies.
• Si une clé est présente dans les deux dictionnaires, sa valeur associée est la somme de ses valeurs dans d1 et d2.
• Si une clé n’est présente que dans un seul dictionnaire, sa valeur associée est la même que dans ce dictionnaire.

⭐ Exemples :

>>> ajoute_dictionnaires({1: 5, 2: 7}, {2: 9, 3: 11})
{1: 5, 2: 16, 3: 11}
>>> ajoute_dictionnaires({}, {2: 9, 3: 11})
{2: 9, 3: 11}
>>> ajoute_dictionnaires({1: 5, 2: 7}, {})
{1: 5, 2: 7}

On considère la fonction separe qui prend en argument un tableau tab dont les éléments sont des 0 et des 1 et qui sépare les 0 des 1 en plaçant les 0 en début de tableau et les 1 à la suite.

Exemples :

>>> separe([1, 0, 1, 0, 1, 0, 1, 0])
[0, 0, 0, 0, 1, 1, 1, 1]
>>> separe([1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0])
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1]

Description des étapes pour tab = [1, 0, 1, 0, 1, 0, 1, 0] :

• Étape 1 : on regarde la première case, qui contient un 1 : on l’échange avec la dernière case.

  tab = [0, 0, 1, 0, 1, 0, 1, 1]

• Étape 2 : la première case contient 0 : elle est bien placée, on avance à la case suivante.

  tab = [0, 0, 1, 0, 1, 0, 1, 1]

• Étape 3 : la seconde case contient 0 : elle est bien placée, on avance.

  tab = [0, 0, 1, 0, 1, 0, 1, 1]

• Étape 4 : la troisième case contient 1 : on l’échange avec l’avant-dernière case.

  tab = [0, 0, 1, 0, 1, 0, 1, 1]

• Et ainsi de suite …

  tab = [0, 0, 0, 0, 1, 1, 1, 1]

On rappelle que :

• le nombre \(a^n\) est le nombre \( a \times a \times ... \times a \), où le facteur \(a\) apparaît \(n\) fois,
• en Python, t[-1] permet d’accéder au dernier élément d’une liste t.

Dans cet exercice, l’opérateur ** et la fonction pow ne sont pas autorisés.

Programme :

• une fonction liste_puissances(a, n) qui prend en paramètres un entier a et un entier strictement positif n, et qui renvoie la liste [a¹, a², …, aⁿ].
• une fonction liste_puissances_borne(a, borne) qui prend en paramètres un entier a ≥ 2 et un entier borne, et qui renvoie la liste des puissances de a, à l’exclusion de \(a^0\), strictement inférieures à borne.

⭐ Exemples :

>>> liste_puissances(3, 5)
[3, 9, 27, 81, 243]
>>> liste_puissances(-2, 4)
[-2, 4, -8, 16]
>>> liste_puissances_borne(2, 16)
[2, 4, 8]
>>> liste_puissances_borne(2, 17)
[2, 4, 8, 16]
>>> liste_puissances_borne(5, 5)
[]

Écrire une fonction recherche_indices_classement qui prend en paramètres un entier elt et une liste d’entiers tab, et qui renvoie trois listes :

• la première liste contient les indices des valeurs de tab strictement inférieures à elt ;
• la deuxième liste contient les indices des valeurs de tab égales à elt ;
• la troisième liste contient les indices des valeurs de tab strictement supérieures à elt.

Exemples :

>>> recherche_indices_classement(3, [1, 3, 4, 2, 4, 6, 3, 0])
([0, 3, 7], [1, 6], [2, 4, 5])
>>> recherche_indices_classement(3, [1, 4, 2, 4, 6, 0])
([0, 2, 5], [], [1, 3, 4])
>>> recherche_indices_classement(3, [1, 1, 1, 1])
([0, 1, 2, 3], [], [])
>>> recherche_indices_classement(3, [])
([], [], [])

On rappelle que les tableaux sont représentés par des listes Python (list).

Le but de cet exercice est d’écrire une fonction ajoute qui prend en paramètres trois arguments indice, element et tab et renvoie un tableau tab_ins dans lequel les éléments sont ceux du tableau tab avec, en plus, l’élément element à l’indice indice.

On considère que les variables indice et element sont des entiers positifs et que les éléments de tab sont également des entiers.

En réalisant cette insertion, Les éléments du tableau tab dont les indices sont supérieurs ou égaux à indice apparaissent décalés vers la droite dans le tableau tab_ins.

Si indice est égal au nombre d’éléments du tableau tab, l’élément element est ajouté dans tab_ins après tous les éléments du tableau tab.

Exemples :

>>> ajoute(1, 4, [7, 8, 9])
[7, 4, 8, 9]
>>> ajoute(3, 4, [7, 8, 9])
[7, 8, 9, 4]
>>> ajoute(0, 4, [7, 8, 9])
[4, 7, 8, 9]

Complète puis teste le code ci-dessous :

On considère la fonction binaire ci-dessous. Cette fonction prend en paramètre un entier positif a en écriture décimale et renvoie son écriture binaire sous la forme d’une chaine de caractères.

L’algorithme utilise la méthode des divisions euclidiennes successives comme l’illustre l’exemple ci-après.

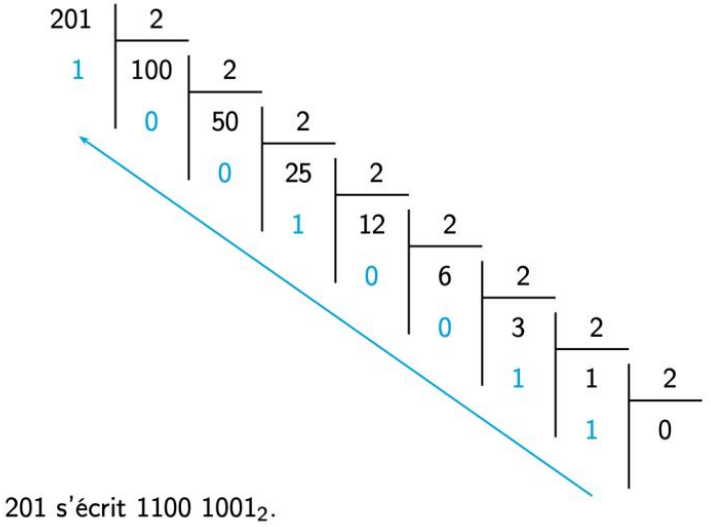
Compléter le code de la fonction binaire.

Exemples :

>>> binaire(83)
'1010011'
>>> binaire(127)
'1111111'
>>> binaire(0)
'0'

Une professeure de NSI décide de gérer les résultats de sa classe sous la forme d’un dictionnaire :

• les clefs sont les noms des élèves ;
• les valeurs sont des dictionnaires dont les clefs sont les types d’épreuves sous forme de chaîne de caractères et les valeurs sont les notes obtenues associées à leurs coefficients dans une liste.

Avec :

resultats = {'Dupont': {
    'DS1': [15.5, 4],
    'DM1': [14.5, 1],
    'DS2': [13, 4],
    'PROJET1': [16, 3],
    'DS3': [14, 4]
    },
    'Durand': {
    'DS1': [6 , 4],
    'DM1': [14.5, 1],
    'DS2': [8, 4],
    'PROJET1': [9, 3],
    'IE1': [7, 2],
    'DS3': [8, 4],
    'DS4':[15, 4]
    }
    }

L’élève dont le nom est Durand a ainsi obtenu au DS2 la note de 8 avec un coefficient 4.

Le professeur crée une fonction moyenne qui prend en paramètre le nom d’un de ses élèves et renvoie sa moyenne arrondie au dixième.

Si l’élève n’a pas de notes, on considère que sa moyenne est nulle. Si le nom donné n’est pas dans les résultats, la fonction renvoie None.

On souhaite programmer une fonction indiquant le point le plus proche d’un point de départ dans un tableau de points non vide. Les points sont tous à coordonnées entières et sont donnés sous la forme d’un tuple de deux entiers. Le tableau des points à traiter est donc un tableau de tuples.

On rappelle que la distance \(d\) entre deux points du plan de coordonnées \((x; y)\) et \((x'; y')\) vérifie la formule :

\( d^2 = (x - x')^2 + (y - y')^2 \)

Compléter le code des fonctions distance_carre et point_le_plus_proche fournies ci-dessous pour qu’elles répondent à leurs spécifications.

Exemples:

>>> distance_carre((1, 0), (5, 3))
25
>>> distance_carre((1, 0), (0, 1))
2
>>> point_le_plus_proche((0, 0), [(7, 9), (2, 5), (5, 2)])
(2, 5)
>>> point_le_plus_proche((5, 2), [(7, 9), (2, 5), (5, 2)])
(5, 2)

On considère la fonction insere ci-dessous qui prend en argument un tableau tab d’entiers triés par ordre croissant et un entier a. Cette fonction crée et renvoie un nouveau tableau tab d’entiers triés par ordre croissant.

Cette fonction crée et renvoie un nouveau tableau à partir de celui fourni en paramètre en y insérant la valeur a de sorte que le tableau renvoyé soit encore trié par ordre croissant. Les tableaux seront représentés sous la forme de listes Python.

Compléter la fonction insere ci-dessous.

Exemples :

>>> insere([1, 2, 4, 5], 3)
[1, 2, 3, 4, 5]
>>> insere([1, 2, 7, 12, 14, 25], 30)
[1, 2, 7, 12, 14, 25, 30]
>>> insere([2, 3, 4], 1)
[1, 2, 3, 4]
>>> insere([], 1)
[1]

Dans cet exercice on cherche à calculer la moyenne pondérée d’un élève dans une matière donnée. Chaque note est associée à un coefficient qui la pondère.

Par exemple, si ses notes sont : 14 avec coefficient 3, 12 avec coefficient 1 et 16 avec coefficient 2, sa moyenne pondérée sera donnée par :

\( \dfrac{14 \times 3 + 12 \times 1 + 16 \times 2}{3+1+2} = 14,333...\)

Écrire une fonction moyenne :

• qui prend en paramètre une liste notes non vide de tuples à deux éléments entiers de la forme (note, coefficient) (int ou float) positifs ou nuls ;
• et qui renvoie la moyenne pondérée des notes de la liste sous forme de flottant si la somme des coefficients est non nulle, None sinon.

Exemple :

>>> moyenne([(8, 2), (12, 0), (13.5, 1), (5, 0.5)])
9.142857142857142
>>> moyenne([(3, 0), (5, 0)])
None

Sur le réseau social TipTop, on s’intéresse au nombre de « like » des abonnés. Les données sont stockées dans des dictionnaires où les clés sont les pseudos et les valeurs correspondantes sont les nombres de « like » comme ci-dessous :

{'Bob': 102, 'Ada': 201, 'Alice': 103, 'Tim': 50}

Écrire une fonction max_dico qui :

• prend en paramètre un dictionnaire dico non vide dont les clés sont des chaînes de caractères et les valeurs associées sont des entiers positifs ou nuls ;
• renvoie un tuple dont :
  • la première valeur est une clé du dictionnaire associée à la valeur maximale ;
  • la seconde valeur est la valeur maximale présente dans le dictionnaire.

Exemples :

>>> max_dico({'Bob': 102, 'Ada': 201, 'Alice': 103, 'Tim': 50})
('Ada', 201)
>>> max_dico({'Alan': 222, 'Ada': 201, 'Eve': 220, 'Tim': 50})
('Alan', 222)

Programmer la fonction multiplication prenant en paramètres deux nombres entiers relatifs n1 et n2, et qui renvoie le produit de ces deux nombres.

Les seules opérations autorisées sont l’addition et la soustraction.

Exemples :

>>> multiplication(3, 5)
15
>>> multiplication(-4, -8)
32
>>> multiplication(-2, 6)
-12
>>> multiplication(-2, 0)
0

On modélise la représentation binaire d'un entier non signé par un tableau d'entiers dont les éléments sont 0 ou 1.

Par exemple, le tableau [1, 0, 1, 0, 0, 1, 1] représente l'écriture binaire de l'entier dont l'écriture décimale est :

$$ 2^6 + 2^4 + 2^1+2^0 = 83 $$

A l'aide d'un parcours séquentiel, écrire la fonction convertir répondant aux spécifications suivantes :

def convertir(tab):
    """
    tab est un tableau d'entiers, dont les éléments sont 0 ou 1,
    et représentant un entier écrit en binaire.
    Renvoie l'écriture décimale de l'entier positif dont la
    représentation binaire est donnée par le tableau tab
    """

Exemples :

>>> convertir([1, 0, 1, 0, 0, 1, 1])
83
>>> convertir([1, 0, 0, 0, 0, 0, 1, 0])
130

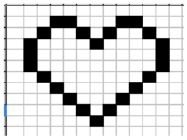
On travaille sur des dessins en noir et blanc obtenus à partir de pixels noirs et blancs. On les représente par une grille de nombres (liste de sous-listes de même longueur) : chaque sous-liste représente une ligne du dessin.

Dans le code ci-dessous, la fonction affiche permet d’afficher le dessin. Les pixels noirs (1 dans la grille) sont représentés par le caractère '*' et les pixels blancs (0 dans la grille) par une espace.

La fonction liste_zoom prend en argument une liste liste_depart et un entier k. Elle renvoie une liste où chaque élément de liste_depart est dupliqué k fois.

La fonction dessin_zoom prend en argument une grille grille et renvoie une nouvelle grille où toutes les lignes de grille sont « zoomées » k fois et répétées k fois.

Compléter les fonctions liste_zoom et dessin_zoom du code suivant :

Exemples :

>>> liste_zoom([1,2,3],3)
[1, 1, 1, 2, 2, 2, 3, 3, 3]

On cherche à déterminer les valeurs du triangle de Pascal (Figure 1). Dans le triangle de Pascal, chaque ligne commence et se termine par le nombre 1. Comme l’illustre la Figure 2, on additionne deux valeurs successives d’une ligne pour obtenir la valeur qui se situe sous la deuxième valeur.

Compléter les fonctions ligne_suivante et pascal ci-dessous. La fonction ligne_suivante prend en paramètre une liste d’entiers ligne correspondant à une ligne du triangle de Pascal et renvoie la liste correspondant à la ligne suivante du triangle de Pascal. La fonction pascal prend en paramètre un entier n et l’utilise pour construire le triangle de Pascal ayant n+1 lignes sous la forme d’une liste de listes.

Exemples :

>>> ligne_suivante([1, 3, 3, 1])
[1, 4, 6, 4, 1]
>>> pascal(2)
[[1], [1, 1], [1, 2, 1]]
>>> pascal(3)
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1]]

On souhaite générer des grilles du jeu de démineur à partir de la position des bombes à placer.

On se limite à la génération de grilles carrées de taille \(n \times n\) où \(n\) est le nombre de bombes du jeu.

Dans le jeu du démineur, chaque case de la grille contient soit une bombe, soit une valeur qui correspond aux nombres de bombes situées dans le voisinage direct de la case (au-dessus, en dessous, à droite, à gauche ou en diagonal : chaque case a donc 8 voisins si elle n'est pas située au bord de la grille).

Voici un exemple de grille \(5 \times 5 \) de démineur dans laquelle la bombe est représentée par une étoile :

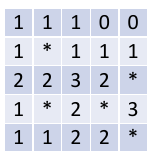
On utilise une liste de listes pour représenter la grille et on choisit de coder une bombe par la valeur -1.

L'exemple ci-dessus sera donc codé par la liste :

[[1,1,1,0,0],
   [1,-1,1,1,1],
   [2,2,3,2,-1],
   [1,-1,2,-1,3],
   [1,1,2,2, -1]]

Compléter le code suivant afin de générer des grilles de démineur, on pourra vérifier que l’instruction genere_grille([(1, 1), (2, 4), (3, 1), (3, 3), (4, 4)]) produit bien la liste donnée en exemple.

On considère la fonction eleves_du_mois prenant en paramètres eleves et notes deux tableaux non vides de même longueur, le premier contenant le nom des élèves et le second, des entiers positifs désignant leur note à un contrôle de sorte que eleves[i] a obtenu la note notes[i].

Cette fonction renvoie le couple constitué de la note maximale attribuée et des noms des élèves ayant obtenu cette note regroupés dans un tableau.

Ainsi, l’instruction eleves_du_mois(['a', 'b', 'c', 'd'], [15, 18, 12, 18]) renvoie le couple (18, ['b', 'd']).

Compléter le code suivant :

Exemples :

>>> eleves_nsi = ['a','b','c','d','e','f','g','h','i','j']
>>> notes_nsi = [30, 40, 80, 60, 58, 80, 75, 80, 60, 24]
>>> eleves_du_mois(eleves_nsi, notes_nsi)
(80, ['c', 'f', 'h'])

L’ordre des gènes sur un chromosome est représenté par un tableau ordre de n cases d’entiers distincts deux à deux et compris entre 1 et n.

Par exemple, ordre = [5, 4, 3, 6, 7, 2, 1, 8, 9] dans le cas n = 9.

On dit qu’il y a un point de rupture dans ordre dans chacune des situations suivantes :

• la première valeur de ordre n’est pas 1 ;
• l’écart entre deux gènes consécutifs n’est pas égal à 1 ;
• la dernière valeur de ordre n’est pas n.

Par exemple, si ordre = [5, 4, 3, 6, 7, 2, 1, 8, 9] avec n = 9, on a

• un point de rupture au début car 5 est différent de 1
• un point de rupture entre 3 et 6 (l’écart est de 3)
• un point de rupture entre 7 et 2 (l’écart est de 5)
• un point de rupture entre 1 et 8 (l’écart est de 7)

Il y a donc 4 points de rupture.

Compléter les fonctions Python est_un_ordre et nombre_points_rupture proposées à la page suivante pour que :

• la fonction est_un_ordre renvoie True si le tableau passé en paramètre représente bien un ordre de gènes de chromosome et False sinon ;
• la fonction nombre_points_rupture renvoie le nombre de points de rupture d’un tableau passé en paramètre représentant l’ordre de gènes d’un chromosome.

Exemples :

>>> est_un_ordre([1, 6, 2, 8, 3, 7])
False
>>> est_un_ordre([5, 4, 3, 6, 7, 2, 1, 8, 9])
True
>>> nombre_points_rupture([5, 4, 3, 6, 7, 2, 1, 8, 9])
4
>>> nombre_points_rupture([1, 2, 3, 4, 5])
0
>>> nombre_points_rupture([1, 6, 2, 8, 3, 7, 4, 5])
7
>>> nombre_points_rupture([2, 1, 3, 4])
2

Le codage de César transforme un message en changeant chaque lettre en la décalant dans l’alphabet. Par exemple, avec un décalage de 3, le A se transforme en D, le B en E, …, le X en A, le Y en B et le Z en C. Les autres caractères (‘!’, ‘?’, …) ne sont pas codés.

La fonction position_alphabet prend en paramètre un caractère lettre et renvoie la position de lettre dans la chaîne de caractères alphabet s’il s’y trouve.

La fonction cesar prend en paramètre une chaîne de caractères message et un nombre entier decalage et renvoie le nouveau message codé avec le codage de César utilisant le décalage decalage.

Compléter la fonction cesar.

Exemples :

>>> cesar('BONJOUR A TOUS. VIVE LA MATIERE NSI !', 4)
'FSRNSYV E XSYW. ZMZI PE QEXMIVI RWM !'
>>> cesar('GTSOTZW F YTZX. ANAJ QF RFYNJWJ SXN !', -5)
'BONJOUR A TOUS. VIVE LA MATIERE NSI !'

On considère une image en 256 niveaux de gris représentée par une grille de nombres, c’est-à-dire une liste de sous-listes toutes de même longueur.

La largeur de l’image est la longueur d’une sous-liste et la hauteur est le nombre de sous-listes.

Chaque sous-liste représente une ligne et chaque élément est un entier entre 0 et 255, l’intensité lumineuse d’un pixel.

Le négatif d’une image est l’image des pixels \(x_n\) tels que \(x_n + x_i = 255\) où \(x_i\) est le pixel correspondant de l’image initiale.

Étant donné une valeur \(seuil\), la binarisation d’une image est l’image des pixels valant \(0\) si \(x_i < seuil\) et \(255\) sinon.

Compléter les fonctions nombre_lignes, nombre_colonnes, negatif et binaire.

Exemples :

>>> img=[[20, 34, 254, 145, 6],
         [23, 124, 237, 225, 69],
         [197, 174, 207, 25, 87],
         [255, 0, 24, 197, 189]]
>>> nombre_lignes(img)
4
>>> nombre_colonnes(img)
5
>>> negatif(img)
[[235, 221, 1, 110, 249], [232, 131, 18, 30, 186], [58, 81, 48, 230, 168], [0, 255, 231, 58, 66]]
>>> binaire(img,120)
[[0, 0, 255, 255, 0],[0, 255, 255, 255, 0],[255, 255, 255, 0, 0],[255, 0, 0, 255, 255]]

La fonction tri_insertion suivante prend en argument un tableau tab (type list) et trie ce tableau en utilisant la méthode du tri par insertion. Compléter cette fonction pour qu’elle réponde à la spécification demandée.

On rappelle le principe du tri par insertion : on considère les éléments à trier un par un, le premier élément constituant, à lui tout seul, un tableau trié de longueur 1. On range ensuite le second élément pour constituer un tableau trié de longueur 2, puis on range le troisième élément pour avoir un tableau trié de longueur 3 et ainsi de suite…

À chaque étape, le premier élément du sous-tableau non trié est placé dans le sous-tableau des éléments déjà triés de sorte que ce sous-tableau demeure trié. Le principe du tri par insertion est donc d’insérer à la n-ième itération, le n-ième élément à la bonne place.

Exemple :

>>> tab = [98, 12, 104, 23, 131, 9]
>>> tri_insertion(tab)
>>> tab
[9, 12, 23, 98, 104, 131]

On considère dans cet exercice un algorithme glouton pour le rendu de monnaie. Pour rendre une somme en monnaie, on utilise à chaque fois la plus grosse pièce possible et ainsi de suite jusqu’à ce que la somme restante à rendre soit nulle.

Les pièces de monnaie utilisées sont :

pieces = [1, 2, 5, 10, 20, 50, 100, 200]

On souhaite écrire une fonction rendu_monnaie qui prend en paramètres :

• un entier somme_due représentant la somme à payer ;
• un entier somme_versee représentant la somme versée qui est supérieure ou égale à somme_due;
• et qui renvoie un tableau de type list contenant les pièces qui composent le rendu de la monnaie restante, c’est-à-dire de somme_versee - somme_due.

Ainsi, l’instruction rendu_monnaie(452, 500) renvoie le tableau [20, 20, 5, 2, 1].

Compléter ce code et le tester.

Exemples :

>>> rendu_monnaie(700, 700)
[]
>>> rendu_monnaie(102, 500)
[200, 100, 50, 20, 20, 5, 2, 1]

On affecte à chaque lettre de l’alphabet un code selon les tableaux ci-dessous :

Cette table de correspondance est stockée dans un dictionnaire dico où les clés sont les lettres de l’alphabet et les valeurs les codes correspondants.

dico = {"A": 1, "B": 2, "C": 3, "D": 4, "E": 5, "F": 6,
        "G": 7, "H": 8, "I": 9, "J": 10, "K": 11, "L": 12,
        "M": 13, "N": 14, "O": 15, "P": 16, "Q": 17,
        "R": 18, "S": 19, "T": 20, "U": 21, "V": 22,
        "W": 23, "X": 24, "Y": 25, "Z": 26}

Pour un mot donné, on détermine d’une part son code alphabétique concaténé, obtenu par la juxtaposition des codes de chacun de ses caractères, et d’autre part, son code additionné, qui est la somme des codes de chacun de ses caractères.

On dit que ce mot est « parfait » si le code additionné divise le code concaténé.

Exemples :

• Pour le mot "PAUL", le code concaténé est la chaîne '1612112', soit l’entier 1 612 112. Son code additionné est l’entier 50 car 16 + 1 + 21 + 12 = 50. 50 ne divise pas 1 612 112. Ainsi, le mot "PAUL" n’est pas parfait.
• Pour le mot "ALAIN", le code concaténé est la chaîne '1121914', soit l’entier 1 121 914. Le code additionné est l’entier 37 car 1 + 12 + 1 + 9 + 14 = 37. 37 divise 1 121 914. Ainsi, le mot "ALAIN" est parfait.

Compléter la fonction codes_parfait qui prend en paramètre un mot en majuscules et renvoie un triplet constitué du code additionné, du code concaténé et d’un booléen indiquant si le mot est parfait ou non. On rappelle que pour tester si un entier b divise un entier a, on utilise l’opérateur modulo a % b ; si a % b vaut 0, alors b divise a.

Exemples :

>>> codes_parfait("PAUL")
(50, 1612112, False)
>>> codes_parfait("ALAIN")
(37, 1121914, True)

La fonction fusion prend deux tableaux tab1, tab2 (type list) d’entiers triés par ordre croissant et les fusionne en un tableau trié tab12 qu’elle renvoie.

Compléter le code de la fonction fusion ci-dessous.

Exemples :

>>> fusion([1,2,3],[])
[1, 2, 3]
>>> fusion([], [])
[]
>>> fusion([1, 6, 10],[0, 7, 8, 9])
[0, 1, 6, 7, 8, 9, 10]

On considère la suite de nombres suivante : 1, 11, 21, 1211, 111221, ….

Cette suite est construite ainsi : pour passer d’une valeur à la suivante, on lit le nombre et on l’écrit sous la forme « nombre de chiffres consécutifs ».

Par exemple, pour 1211 : on lit un 1, un 2, deux 1, donc on écrit 1 1, 1 2, 2 1, puis on concatène 111221.

Compléter la fonction nombre_suivant(s) qui prend en entrée un nombre sous forme de chaîne et renvoie le nombre suivant par ce procédé (toujours sous forme de chaîne).

Exemples :

>>> nombre_suivant('1211')
'111221'
>>> nombre_suivant('311')
'1321'

Un nombre premier est un entier naturel qui admet exactement deux diviseurs entiers et positifs : 1 et lui-même.

Le crible d’Ératosthène permet de déterminer les nombres premiers plus petits qu’un certain nombre n strictement supérieur à 1.

On considère un tableau tab de booléens (type list), initialement tous égaux à True, sauf tab[0] et tab[1] qui valent False, 0 et 1 n’étant pas des nombres premiers. On parcourt alors ce tableau de gauche à droite et, pour chaque indice i :

• si tab[i] vaut True : le nombre i est premier et on met à False toutes les cases d’indice multiple de i, à partir de 2*i (2*i, 3*i, …) ;
• si tab[i] vaut False : le nombre i n’est pas premier et on ne change rien.

Compléter la fonction crible(n) qui renvoie la liste de tous les nombres premiers strictement inférieurs à n.

Exemples :

>>> crible(40)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37]
>>> crible(5)
[2, 3]

La fonction tri_bulles prend en paramètre un tableau tab d’entiers (type list) et le modifie pour le trier par ordre croissant.

Le tri à bulles est un tri en place qui commence par placer le plus grand élément en dernière position en parcourant le tableau de gauche à droite et en échangeant au passage les éléments voisins mal ordonnés (si la valeur de l’élément d’indice i a une valeur strictement supérieure à celle de l’indice i + 1, ils sont échangés). Le tri place ensuite en avant-dernière position le plus grand élément du tableau privé de son dernier élément en procédant encore à des échanges d’éléments voisins. Ce principe est répété jusqu’à placer le minimum en première position.

Exemple : pour trier le tableau [7, 9, 4, 3] :

• première étape : 7 et 9 ne sont pas échangés, puis 9 et 4 sont échangés, puis 9 et 3 sont échangés, le tableau est alors [7, 4, 3, 9]
• deuxième étape : 7 et 4 sont échangés, puis 7 et 3 sont échangés, le tableau est alors [4, 3, 7, 9]
• troisième étape : 4 et 3 sont échangés, le tableau est alors [3, 4, 7, 9]

Compléter le code Python ci-dessous qui implémente la fonction tri_bulles.

Exemples :

>>> tab = []
>>> tri_bulles(tab)
>>> tab
[]
>>> tab2 = [9, 3, 7, 2, 3, 1, 6]
>>> tri_bulles(tab2)
>>> tab2
[1, 2, 3, 3, 6, 7, 9]
>>> tab3 = [9, 7, 4, 3]
>>> tri_bulles(tab3)
>>> tab3
[3, 4, 7, 9]

On considère dans cet exercice l’élection d’un vainqueur à l’issue d’un vote. Les résultats du vote sont stockés dans un tableau : chaque vote exprimé est le nom d’un ou d’une candidate.

Par exemple, les résultats pourraient correspondre au tableau :

urne = ['A', 'A', 'A', 'B', 'C', 'B', 'C', 'B', 'C', 'B']

indiquant que 3 candidats ont obtenu au moins un vote chacun : A, B et C.

On cherche à déterminer le ou les candidats ayant obtenu le plus de suffrages. Pour cela, on propose d’écrire deux fonctions :

• la fonction depouille doit permettre de compter le nombre de votes exprimés pour chacune des issues. Elle prend en paramètre un tableau et renvoie le résultat dans un dictionnaire dont les clés sont les noms des issues et les valeurs le nombre de votes en leur faveur ;
• la fonction vainqueurs doit désigner le nom du ou des gagnants. Elle prend en paramètre un dictionnaire non vide dont la structure est celle du dictionnaire renvoyé par la fonction depouille et renvoie un tableau. Ce tableau peut contenir plusieurs éléments s’il y a des artistes ex-aequo.

Compléter les fonctions depouille et vainqueurs ci-après pour qu’elles renvoient les résultats attendus.

Exemples d’utilisation :

>>> depouille([ 'A', 'B', 'A' ])
{'A': 2, 'B': 1}
>>> depouille([])
{}
>>> election = depouille(['A', 'A', 'A', 'B', 'C', 'B', 'C', 'B', 'C', 'B'])
>>> election
{'A': 3, 'B': 4, 'C': 3}
>>> vainqueurs(election)
['B']
>>> vainqueurs({ 'A' : 2, 'B' : 2, 'C' : 1})
['A', 'B']

Soit une image binaire représentée dans un tableau à 2 dimensions. Les éléments M[i][j], appelés pixels, sont égaux soit à 0 soit à 1.

Une composante d’une image est un sous-ensemble de l’image constitué uniquement de 1 et de 0 qui sont côte à côte, soit horizontalement soit verticalement.

Par exemple, les composantes de

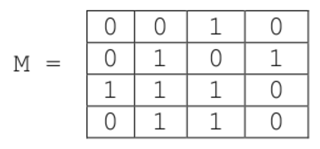
sont

On souhaite, à partir d’un pixel égal à 1 dans une image M, donner la valeur val à tous les pixels de la composante à laquelle appartient ce pixel.

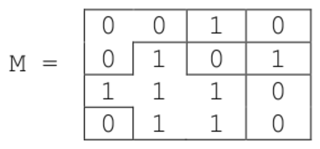
La fonction colore_comp1 prend pour paramètre une image M (représentée par une liste de listes), deux entiers i et j et une valeur entière val. Elle met à la valeur val tous les pixels de la composante du pixel M[i][j] s’il vaut 1 et ne fait rien sinon.

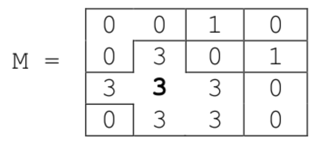
Par exemple, colore_comp1(M, 2, 1, 3) donne

Compléter le code récursif de la fonction colore_comp1.

Exemple :

>>> M = [[0, 0, 1, 0], [0, 1, 0, 1], [1, 1, 1, 0], [0, 1, 1, 0]]
>>> colore_comp1(M, 2, 1, 3)
>>> M
[[0, 0, 1, 0], [0, 3, 0, 1], [3, 3, 3, 0], [0, 3, 3, 0]]

On considère au plus 26 personnes A, B, C, D, E, F … qui peuvent s’envoyer des messages avec deux règles à respecter :

• chaque personne ne peut envoyer des messages qu’à une seule personne (éventuellement elle-même),
• chaque personne ne peut recevoir des messages qu’en provenance d’une seule personne (éventuellement elle-même).

Voici un exemple - avec 6 personnes - de « plan d’envoi des messages » qui respecte les règles ci-dessus, puisque chaque personne est présente une seule fois dans chaque colonne :

• A envoie ses messages à E
• E envoie ses messages à B
• B envoie ses messages à F
• F envoie ses messages à A
• C envoie ses messages à D
• D envoie ses messages à C

Le dictionnaire correspondant à ce plan d’envoi est alors le suivant :

plan_a = {'A':'E', 'B':'F', 'C':'D', 'D':'C', 'E':'B', 'F':'A'}

Un cycle est une suite de personnes dans laquelle la dernière est la même que la première.

Sur le plan d’envoi plan_a des messages ci-dessus, il y a deux cycles distincts : un premier cycle avec A, E, B, F et un second cycle avec C et D.

En revanche, le plan d’envoi plan_b ci-dessous :

plan_b = {'A':'C', 'B':'F', 'C':'E', 'D':'A', 'E':'B', 'F':'D'}

comporte un unique cycle : A, C, E, B, F, D. Dans ce cas, lorsqu’un plan d’envoi comporte un unique cycle, on dit que le plan d’envoi est cyclique.

Pour savoir si un plan d’envoi de messages comportant N personnes est cyclique, on peut utiliser l’algorithme ci-dessous :

• on part d’un expéditeur (ici A) et on inspecte son destinataire dans le plan d’envoi,
• chaque destinataire devient à son tour expéditeur, selon le plan d’envoi, tant qu’on ne « retombe » pas sur l’expéditeur initial,
• le plan d’envoi est cyclique si on l’a parcouru en entier.

Compléter la fonction est_cyclique en respectant la spécification. On rappelle que la fonction Python len permet d’obtenir la longueur d’un dictionnaire.

Exemples :

>>> est_cyclique({'A':'E','F':'A','C':'D','E':'B','B':'F','D':'C'})
False
>>> est_cyclique({'A':'E','F':'C','C':'D','E':'B','B':'F','D':'A'})
True
>>> est_cyclique({'A':'B','F':'C','C':'D','E':'A','B':'F','D':'E'})
True
>>> est_cyclique({'A':'B','F':'A','C':'D','E':'C','B':'F','D':'E'})
False